Polynomial Representation Part 1🕐
When you think about representing polynomials using an array, you might think it’s easy. We just need to have the degree of the polynomial and enter the coefficients. Isn’t that right? But is that memory efficient?🤔 Nope, because there would be spaces wasted. Wait a minute! But what’s a polynomial? Yes! you got it right. Let’s dive deep into this!
What’s a polynomial?
A polynomial p(x) is the expression in variable x which is in the form , where a, b, c …., k fall in the category of real numbers and ‘n’ is a non-negative integer, which is called the degree of a polynomial. For an algebraic expression to be a polynomial, all of the exponents in it must be non-negative integers. If an algebraic expression contains a radical, it isn’t a polynomial, as a general rule.
An essential characteristic of the polynomial is that each term in the polynomial expression consists of two parts:
- one is the coefficient
- other is the exponent
For example, ${5x^2+2x+3}$ Here,2 is the degree of the polynomial.
- coefficients of = 5,2
- exponents=2,1
Representation of a polynomial can be done in two ways
- Arrays
- Linked Lists
In part 1, we will be talking about representation using arrays. The operations such as addition, subtraction, multiplication, differentiation and so forth can be performed on the polynomials represented as arrays.
ALGORITHM
Let’s look at the algorithm of polynomial addition where we can learn how to represent a polynomial using an array and add two polynomials and store the result in the same array itself.
The algorithm works by comparing terms from the two polynomials until one or both polynomials become empty.
The comparison is performed and the result is added to the resultant polynomial.
If one of the polynomials becomes empty, the remaining terms from the other polynomial is copied to the sum polynomial.
C IMPLEMENTATION
#define MAXTERMS 100
typedef struct{
float coeff;
int expon;
}polynomial;
polynomial terms[MAXTERMS];
int avail=0;
Here, we have added a structure consisting of coefficient and exponent of polynomial.avail which points the available is set to 0. Let’s build the concept together! We need to compare the exponents and arrange the resultant expression.
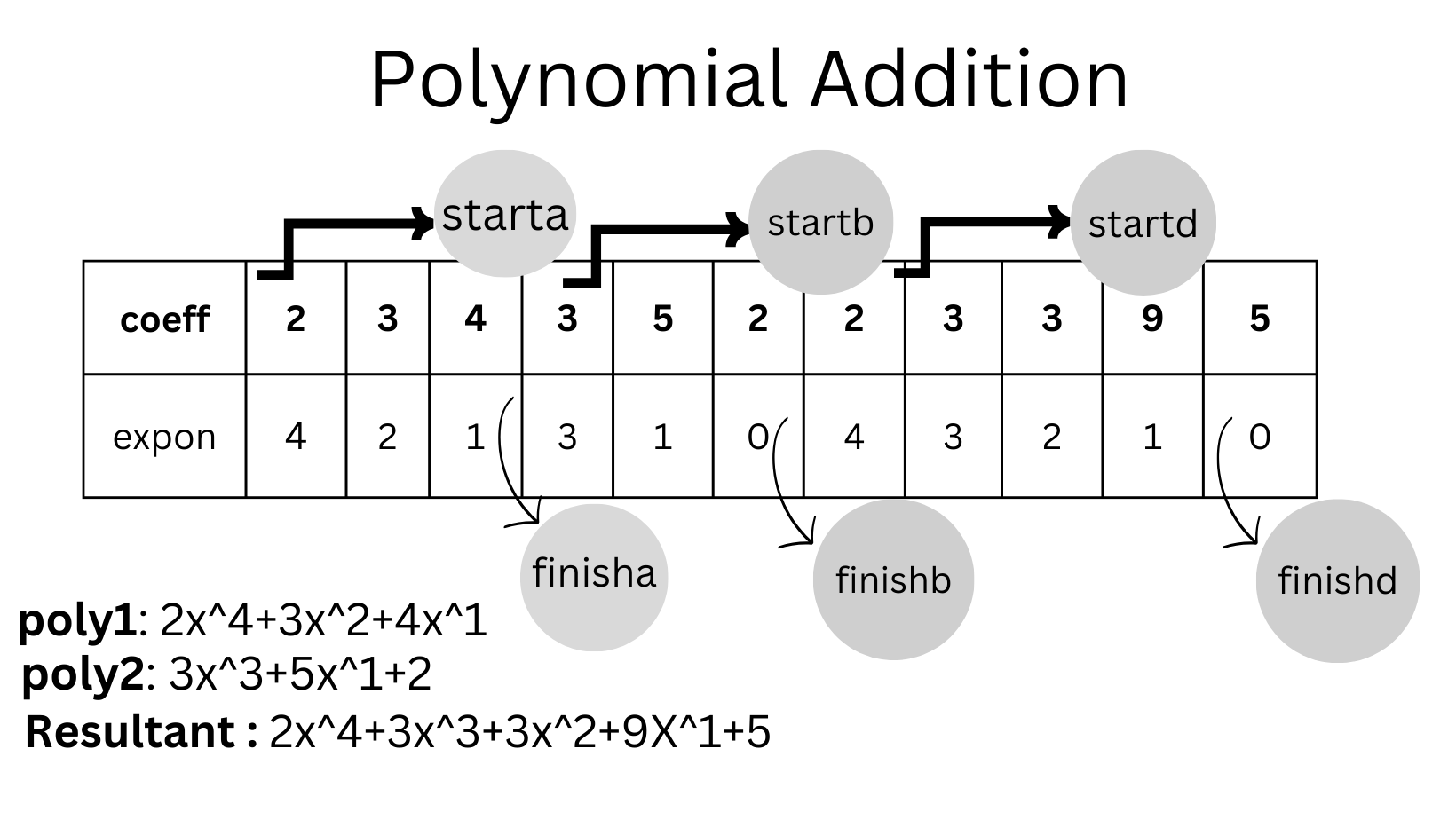
Algorithm Polyadd(startA, finishA, startB, finishB,startD, *finishD)
Start
startd=avail
While(startA <=finishA && startB<= finishB)
If (terms[startA].expon < terms[startB].expon)
attach(terms[startB].coeff,terms[startB].expon)
startB++
Else if (terms[startA].expon > terms[startB].expon)
attach(terms[startA].coef,terms[startA].expon)
startA++
Else
coefficient=terms[startA].coeff+terms[startB].coeff
If (coefficient)
attach(coefficient, terms[startA].expon)
endif
startA++
startB++
end if
endwhile
We may have missed some terms so let’s add them too!
While (startA<=finishA)
attach(terms[startA].coeff,terms[startA].expon)
startA++
endwhile
While(startB<=finishB)
attach(terms[startB].coeff,terms[startB].expon)
startB++
endwhile
*finishD=avail-1
Stop
Now let’s define the attach algorithm.
Algorithm attach(coefficient, exponent)
Start
If (avail>=MAX-TERMS)
print (“Too many terms”)
exit
Endif
terms[avail].coeff=coefficient
terms[avail].expon=exponent
avail++
Stop
Let’s look at the code! It’s written in C.
#include<stdio.h>
#include<math.h>
#define max 100
typedef struct{
float coeff;
int exp;
}poly;
poly terms[max];
int avail=0;
int starta,startb,finisha,finishb,startd,finishd;
void polyadd(int starta,int startb,int finisha,int finishb,int startd,int * finishd);
void attach(float coeff , int exp , int index);
int main()
{
int i;
starta=avail;
printf("Enter the number of terms in polynomial1:");
scanf("%d",&finisha);
finisha--;
printf("\nEnter the coeffecients and exponents in DESCENDING order");
for(i = starta ; i<=finisha; i++)
{
printf("\nCoeffecient :");
scanf("%f",&terms[i].coeff);
printf("Exponent :");
scanf("%d", &terms[i].exp);
avail++;
}
printf("Enter the number of terms in polynomial2:");
scanf("%d",&i);
finishb = finisha + i;
printf("\nEnter the coeffecients and exponents in DESCENDING order");
for(i = finisha+1 ; i<=finishb; i++)
{
printf("\nCoeffecient :");
scanf("%f", &terms[i].coeff);
printf("Exponent :");
scanf("%d", &terms[i].exp);
avail++;
}
//printing first polynomial
printf("\nExpression 1 = %.2fx^%d " , terms[0].coeff , terms[0].exp);
for(i=1;i<=finisha;i++)
{
printf("+ %.2fx^%d",terms[i].coeff,terms[i].exp);
}
//printing second polynomial
printf("\nExpression 2 = %.2fx^%d " ,terms[finisha+1].coeff , terms[finisha+1].exp );
for(i=finisha+2;i<=finishb;i++)
{
printf("+ %.2fx^%d",terms[i].coeff,terms[i].exp);
}
printf("\n");
startd = avail;
finishd = avail-1;
startb = finisha+1;
polyadd(starta,startb,finisha,finishb,startd, &finishd);
printf("The resultant expression is: %.2fx^%d" , terms[startd].coeff , terms[startd].exp );
for(i=startd+1;i<=finishd;i++){
printf("+ %.2fx^%d ",terms[i].coeff,terms[i].exp);
}
printf("\n");
return 0;
}
void polyadd(int starta,int startb,int finisha,int finishb,int startd,int* finishd){
while(starta<=finisha && startb<=finishb)
{
if(terms[starta].exp == terms[startb].exp)
{
float coefficient = terms[startb].coeff + terms[starta].coeff;
if(coefficient){
attach(coefficient, terms[startb].exp, startd);
starta++;
startb++;
startd++;
*finishd = *finishd +1 ;
}
}
else if (terms[starta].exp > terms[startb].exp) {
attach(terms[starta].coeff, terms[starta].exp, startd);
starta++;
startd++;
*finishd = *finishd +1 ;
}
else if (terms[starta].exp < terms[startb].exp) {
attach(terms[startb].coeff, terms[startb].exp, startd);
startb++;
startd++;
*finishd = *finishd +1 ;
}
}
while(starta<=finisha)
{
attach(terms[starta].coeff, terms[starta].exp, startd);
starta++;
startd++;
*finishd = *finishd +1 ;
}
while(startb<=finishb)
{
attach(terms[startb].coeff, terms[startb].exp, startd);
startb++;
startd++;
*finishd = *finishd +1 ;
}
}
void attach(float coeff , int exp , int index)
{
terms[index].coeff = coeff;
terms[index].exp = exp;
}
Let’s meet with Polynomial representation using Linked List in the next part!
